A 'mesh' (also called a loop) is simply a path through a circuit that starts and ends at the same place. For the purpose of mesh analysis, a mesh is a loop that does not enclose other loops.
Similar to nodal analysis, mesh analysis is a formalized procedure based on KVL equations. A caveat: mesh analysis can only be used on 'planar' circuits (i.e. there are no crossed, but unconnected, wires in the circuit diagram.)
1. Draw circuit in planar form (if possible.)
2. Identify meshes and name mesh currents. Mesh currents should be in the clockwise direction. The current in a branch shared by two meshes is the difference of the two mesh currents.
3. Write a KVL equation in terms of mesh currents for each mesh.
4. Solve the resulting system of equations.
1. Dependent Voltage Sources
Solution: Same procedure, but write the dependency variable in terms of mesh currents.
2. Independent Current Sources
Solution: If current source is not on a shared branch, then we have been given one of the mesh currents! If it is on a shared branch, then use a 'super-mesh' that encircles the problem branch. To make up for the mesh equation you lose by doing this, use the mesh current relationship implied by the current source (i.e. I 2 − I 1 = 4 m A -I_=4mA> ).
3. Dependent Current Sources
Solution: Same procedure as for an independent current source, but with an extra step to eliminate the dependency variable. Write the dependency variable in terms of mesh currents.

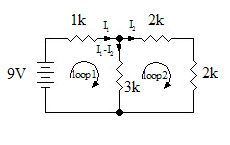
Given the Circuit below, find the currents I 1 > , I 2 > .
The circuit has 2 loops indicated on the diagram. Using KVL we get:
Loop1: 0 = 9 − 1000 I 1 − 3000 ( I 1 − I 2 ) -3000(I_-I_)>
Loop2: 0 = 3000 ( I 1 − I 2 ) − 2000 I 2 − 2000 I 2 <\displaystyle 0=3000(I_-I_)-2000I_-2000I_>
Simplifying we get the simultaneous equations:
0 = 9 − 4000 I 1 + 3000 I 2 <\displaystyle 0=9-4000I_+3000I_>
0 = 0 + 3000 I 1 − 7000 I 2 <\displaystyle 0=0+3000I_-7000I_>
solving to get:
I 1 = 3.32 m A =3.32mA>
I 2 = 1.42 m A =1.42mA>