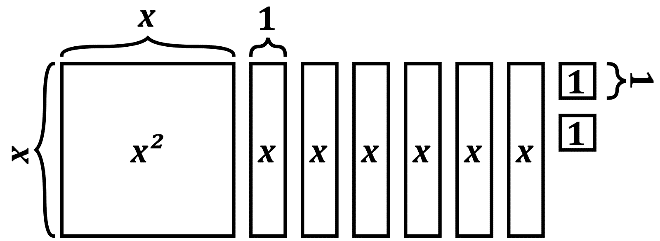
Hi, and welcome to this video on the process of Completing the Square. This algebraic process is important in the study of quadratic equations and their key features. Specifically, completing the square helps us to identify the vertex of a quadratic graph and allows us to find the roots of a quadratic equation using the “square root” method. In this video, we will explore this process and work through some example problems to give you some practice.
As mentioned, the process of completing the square allows us to identify the vertex of a quadratic, which is either the maximum or minimum value of the function. Before we attack the process, let’s review the basics of quadratic functions and their graphs.
Graphs of quadratic functions are called parabolas. The vertex of a parabola is either the maximum or minimum value of the function. If the parabola opens “up”, the vertex is the minimum point of the function and can be visualized as the bottom of a valley. If the function opens “down”, the vertex is the maximum point of the function, as if it were on the top of a hill.
There are many applications that require the knowledge of where a function is at its maximum or minimum value, so being able to identify this point quickly is an important skill.
Quadratic equations are typically written in standard form, \(y=ax^2+bx+c\), where c is a constant that identifies the y-intercept of the graph at (0, c). This point is useful for graphing the function, but it does not tell us where the graph will reach its maximum or minimum value. This is where the “completing the square” process comes in. The process of completing the square results in a quadratic written in vertex form. As the name suggests, it is the vertex, notated (h, k), that is clearly identifiable: \(y=a(x-h)^2+k\).
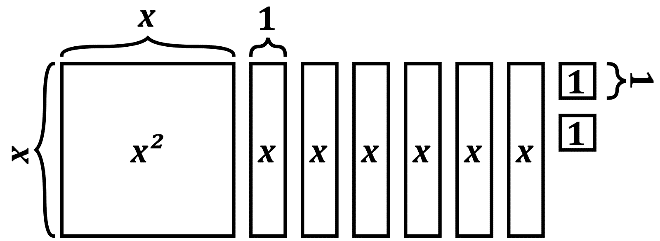
Consider this visual for the standard-form quadratic expression, \(x^2+6x+2\):
Do you see how this relates to the expression? The leading term is \(x^2\), there are a total of six x terms, and there are two “1” terms.
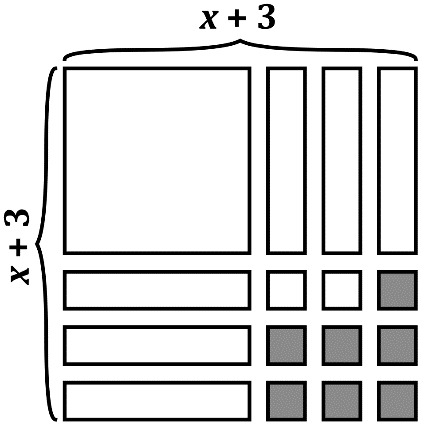
Suppose we were asked to change this rectangular arrangement to take the shape of a square. Well, because there are six “x” terms, we could move half of them below the \(x^2\), as shown here:
We can also move the two “1’s” into place to fill in the lower right corner of the square. But there aren’t enough “1” terms! In order to complete the square configuration, we would have to add seven additional “1’s”, as shown in dark blue.
Nice! We have created a perfect square, but now we have to account for the seven “1’s” that we had to add in order to complete the square. Fortunately, it is a simple adjustment of subtracting the seven “1’s” from the squared binomial, like so: \((x+3)^2-7\). In other words, we would add 7 to create a perfect square, but then we had to subtract 7 to keep the expressions equivalent.
The result is the vertex form of the quadratic expression, \((x+3)^2-7\).
To check our work, we simplify the vertex form expression as follows:
Step 1: Expand the squared binomial term. Our vertex form was: \((x+3)^2-7\).So we wanna expand the \((x+3)^2\) to be \((x+3)(x+3)-7\).
Step 2: Multiply the binomials. We’ll get \(x^2+3x+3x+9-7\).
Step 3: Combine like terms in the expression. \(x^2+3x+3x+9-7\)
Here we can combine our 3x and our 3x, so we’ll have \(x^2+6x\), and then 9-7 is +2.
This result is the original standard-form expression, so we know that our work is correct!
Here is another visual example problem for you to check your understanding of the completing the square process.
First, we need to write the standard form quadratic expression that matches this visual.
Then, we need to figure out how many yellow boxes are needed to complete the square. In this case, it’s two.
Now, we need to write the vertex-form quadratic expression. Remember, we’ll need to adjust the expression to remove the yellow blocks that were needed to complete the square!
So this gives us \((x+2)^2-2\).
Finally, let’s check our work by multiplying the binomials and combining like terms. We have our \((x+2)^2-2\), which we then expand out to be \((x+2)(x+2)-2\). We FOIL to multiply these two expressions out.
And simplify. \(x^2\) plus, \(2x+2x\) gives us 4x, and 4-2 gives us +2.
\(x^2+4x+2\)
As we can see, our answer does match the standard-form result.
Now let’s tackle the algebraic work of completing the square. The goal is to create a “perfect square trinomial” from the coefficients of the standard form quadratic. Perfect square trinomials factor to either \((x+h)^2\) or \((x-h)^2\), where “h” is the coefficient of the x-term divided in half.
Let’s practice building a perfect square trinomial before moving on. Suppose you have a quadratic expression, \(x^2+6x\). In order to create the perfect square trinomial, we divide the coefficient of the x-term by 2 and square the result, \(\frac^2\), for a value of 9. When we add this value to the original expression, we have a perfect square trinomial, \(x^2+6x+9\), which factors to \((x+3)^2\). Recall that this is the same strategy that was used with the visual representation of completing the square. We would’ve had to add nine “1’s” to complete the lower right corner of the square.
Now for the adjustment for adding those 9 squares: Just as we did before, simply subtract the value that was added from the squared binomial, \((x+3)^2-9\). You have just converted a standard-form quadratic expression into vertex form!
Let’s work through another example problem.
Rewrite the standard form quadratic equation, \(y=x^2-4x-7\), in vertex form by completing the square.
First, identify the coefficients a, b, and the constant, c. a = 1, b = -4, c = -7.
For now, we will ignore the constant, -7, and create the perfect square trinomial with the \(x^2\) and \(-4x\) terms.
Next, determine the value needed to create the perfect square trinomial,\((\frac)^2\), which simplifies to \((-2)^2\), which equals 4.
Now, add 4 to the first two terms to create the perfect square: \(y=x^2-4x+4-7\)
Then, factor the perfect square trinomial that you created: \(y=(x-2)^2-7\)
Adjust the expression by subtracting 4: \(y=(x-2)^2-7-4\)
Finally, simplify to show the quadratic equation in vertex form: \(y=(x-2)^2-11\)
Matching up this vertex form equation with the general form, \(y=a(x-h)^2+k\), indicates that the coefficient, \(a=1\), and the vertex of the parabola is at the ordered pair, \((2, -11)\). Because a>0, the parabola opens “up”, meaning that the vertex is the minimum value of the function. As you can probably guess, when a Show Answer
Answer:Normally you will see quadratic equations in standard form \(y=ax^2+bx+c\). However, quadratic equations can also be written in vertex form. The benefit of vertex form is that the vertex of the parabola \((h,k)\) is clearly identifiable. Vertex form: \(y=a(x-h)^2+k\)
Hide Answer Question #2:
The following quadratic is written in vertex form. What is the vertex of the parabola?